Tampaknya saat ini kita telah memasuki musim penghujan. Waktu yang tersedia bagi saya untuk melatih tembakan saya di halaman semakin terbatas dan beberapa materi observasional harus menunggu juga sampai perbaikan performa senapan saya dikerjakan. Waktu yang tepat untuk memikirkan dan belajar suatu topik yang lebih berat. Pada artikel kali ini saya berusaha memahami misteri kecepatan mimis dan istilah ballistic coefficient. Jujur banyak kesulitan dalam saya mempelajari materi ini karena seperti yang saya katakan sebelumnya; saya alergi dengan berbagai rumus matematika dan fisika. Namun demi memberi pengertian yang lengkap dan benar saya coba mencernanya pelan-pelan. Sebagian besar artikel saya kali ini saya ambil dari tulisan Profesor Mike Wright dalam kolom Technical Airgun dari majalah Airgun Sport yang entah diterbitkan pada edisi yang mana. Selengkapnya dapat anda unduh pada situs ini.
Karena ternyata pokok bahasan ini sangat sulit untuk saya ringkas, saya akan memecah pokok bahasan ini ke dalam beberapa bagian.
Dalam referat saya kali ini saya mencoba menjawab pertanyaan dan penasaran saya terhadap kecepatan proyektil (dalam hal ini adalah mimis) dalam berbagai jarak dan faktor-faktor apa saja yang mempengaruhi kecepatan tersebut.
Sebelum memahami apa saja yang mempengaruhi kecepatan mimis, saya harus mengetahui bagaimana kecepatan suatu mimis dibentuk. Dalam penelusuran saya didapati bahwa mimis bergerak maju karena:
1. Perbedaan tekanan udara antara bagian belakang (rok mimis) dan bagian depan mimis (kepala mimis).
2. Momentum yang diterima mimis akibat bertubrukan dengan benda yang memiliki massa dan kecepatan yang lebih besar darinya.
Karena ternyata pokok bahasan ini sangat sulit untuk saya ringkas, saya akan memecah pokok bahasan ini ke dalam beberapa bagian.
***
Pernahkah anda berpikir kapankah saatnya mimis mencapai kecepatan maksimalnya? Saya selalu memikirkannya saat pertama kali mempelajari senapan angin. Berpikir dan berasumsi dengan konsep fisika klasik pada gerakan parabolik benda (berdasarkan kenangan buruk saya pada soal-soal fisika semasa SMU), saya selalu berkhayal bahwa suatu mimis masih mengalami percepatan/akselerasi sepanjang lintasannya. Tapi ternyata saya salah paham. Konsep antara gerakan parabolik pada suatu benda yang diluncurkan dan pada suatu proyektil senjata api/senapan angin ternyata berbeda. Bahkan studi fenomena ini sudah menjadi suatu disiplin ilmu khusus yang digolongkan dalam studi transitional ballistic/intermediate ballistic yang merupakan bagian dari external ballistic.Dalam referat saya kali ini saya mencoba menjawab pertanyaan dan penasaran saya terhadap kecepatan proyektil (dalam hal ini adalah mimis) dalam berbagai jarak dan faktor-faktor apa saja yang mempengaruhi kecepatan tersebut.
Sebelum memahami apa saja yang mempengaruhi kecepatan mimis, saya harus mengetahui bagaimana kecepatan suatu mimis dibentuk. Dalam penelusuran saya didapati bahwa mimis bergerak maju karena:
1. Perbedaan tekanan udara antara bagian belakang (rok mimis) dan bagian depan mimis (kepala mimis).
Prinsip ini berlaku pada senapan pneumatik (dalam hal ini senapan multipump/uklik dan PCP/senapan gas dan berlaku juga untuk senapan gejluk). Semakin tinggi selisih tekanan dan semakin lama selisih tekanan ini berlangsung, maka semakin tinggi kecepatan yang akan dihasilkan. Untuk menciptakan kedua faktor tersebut, maka sebuah mimis harus membentuk seal yang rapat pada bagian rok-nya dan harus melewati suatu tabung di mana tabung ini harus cukup panjang untuk mimis berakselerasi. Setelah melewati ujung tabung ini (yaitu ujung laras), mimis tidak lagi mengalami akselerasi karena gaya pendorongnya yang berupa perbedaan tekanan udara telah hilang. Dikatakan semakin panjang suatu laras, maka kecepatan yang dihasilkan pada senapan jenis pneumatik ini akan semakin tinggi. Hal ini berhubungan dengan banyaknya waktu yang dialami mimis dalam perbedaan tekanan tersebut sehingga memberi kesempatan lebih lama untuk berakselerasi dan mencapai kecepatan tertingginya. Sudah banyak bukti yang menerangkan teori ini. Salah satu favorit saya pada senapan angin adalah data ini.
| Gambar 1. Tabel perbandingan kekuatan per hammer (Kolom Kiri) pada senapan Airforce Talon dengan kecepatan yang dihasilkannya menggunakan 3 panjang laras yang berbeda (Kolom Atas, dalam inchi). Diambil dari http://www.pyramydair.com/blog/2013/08/testing-the-effect-of-barrel-length-on-a-precharged-rifle/ |
Perbedaan tekanan di belakang rok mimis ini sendiri diciptakan dari pemuaian udara yang dimampatkan sebelumnya. Sifat kecepatan pemuaian udara, peningkatan volume, dan tekanan akhir gas ini juga berbeda-beda antara: udara atmosfer, CO2, maupun gas lain seperti propana (mis. green gas, pada airsoft gun).
Gaya penyeimbang yang berlaku pada mimis ini adalah hambatan udara dan terutama adalah friksi/gaya gesek dengan tabung (dalam hal ini permukaan rifling laras).
Kemampuan meracik tekanan udara dan panjang laras adalah faktor utama yang menentukan kecepatan mimis sebuah senapan di atas faktor penentu lainnya. Isu ini ditunjukkan pula pada data di atas di mana pada kekuatan udara yang terlalu lemah, panjangnya laras justru memberi kerugian.
2. Momentum yang diterima mimis akibat bertubrukan dengan benda yang memiliki massa dan kecepatan yang lebih besar darinya.
Prinsip ini berlaku pada senapan spring-piston/per di mana sebuah mimis dihantam oleh sebuah piston/seher yang memiliki massa jauh lebih berat dan kecepatan lebih tinggi. Piston ini sendiri mendapatkan energinya dari pelepasan energi potensial sebuah per yang dikompresikan. Dalam proses ini kolom udara terbentuk dan kolom ini berfungsi sebagai bantalan (air cushion) untuk menghantarkan energi benturan secara merata pada permukaan rok mimis dan mencegah piston secara langsung membentur bagian ujung tabung kompresi/reciever.
Pada mekanisme ini akselerasi mimis terjadi sangat cepat dan menurut Gerald Cardew (penulis buku "Airgun: From Trigger to Target") mimis telah mencapai puncak kecepatannya pada 6" pertama dihitung dari pangkal laras. Maka dalam hal ini, bila gaya penyeimbang yang diterima mimis yang bergerak adalah sama yaitu friksi, panjang laras adalah suatu kerugian karena melewati batas akselerasinya hanya akan meninggalkan gaya gesek/friksi pada mimis. Oleh karena itu para perancang senapan angin jenis spring-piston ini biasanya memilih laras yang relatif lebih pendek daripada senapan angin berjenis pneumatik.
Sesaat setelah mimis meninggalkan laras dikatakan terdapat gaya (force) fisika lain yang mempengaruhi laju dan arah mimis. Gaya yang berperan mempengaruhi laju dan gerak mimis setelah meninggalkan laras adalah gaya gravitasi dan hambatan udara (air drag). Gaya gravitasi selalu mengarahkan mimis ke arah pusat bumi (ke bawah) sedangkan hambatan udara dapat menggerakan mimis ke segala arah tergantung arah dan kecepatan angin. Karena hambatan udara sendiri terutama bersifat sebagai counter-force terhadap gaya gerak mimis (gaya yang melawan, sesuai Hukum Ketiga Newton tentang Aksi-Reaksi), maka mimis akan segera mengalami deselerasi setelah meninggalkan laras.
Dikatakan bahwa deselerasi yang dialami oleh mimis ini berada dalam rasio yang konstan. Artinya untuk setiap jarak yang ditempuh oleh mimis terdapat suatu angka pengurang kecepatan yang tetap. Sebagai contoh: sebuah mimis yang bergerak 600 fps diukur pada ujung larasnya ternyata menunjukkan kecepatan 492 fps pada 10 meter pertama (berarti kecepatannya berkurang 18%), maka bila diukur pada 20 meter mimis ini akan memiliki kecepatan 403 fps (berkurang lagi sebanyak 18%) dan bila diukur lagi pada 30 meter mimis ini akan memiliki kecepatan 337 (berkurang lagi 18%). Pengurangan kecepatan ini terjadi dengan pola yang tetap dan bersifat eksponensial.
Pada mekanisme ini akselerasi mimis terjadi sangat cepat dan menurut Gerald Cardew (penulis buku "Airgun: From Trigger to Target") mimis telah mencapai puncak kecepatannya pada 6" pertama dihitung dari pangkal laras. Maka dalam hal ini, bila gaya penyeimbang yang diterima mimis yang bergerak adalah sama yaitu friksi, panjang laras adalah suatu kerugian karena melewati batas akselerasinya hanya akan meninggalkan gaya gesek/friksi pada mimis. Oleh karena itu para perancang senapan angin jenis spring-piston ini biasanya memilih laras yang relatif lebih pendek daripada senapan angin berjenis pneumatik.
Sesaat setelah mimis meninggalkan laras dikatakan terdapat gaya (force) fisika lain yang mempengaruhi laju dan arah mimis. Gaya yang berperan mempengaruhi laju dan gerak mimis setelah meninggalkan laras adalah gaya gravitasi dan hambatan udara (air drag). Gaya gravitasi selalu mengarahkan mimis ke arah pusat bumi (ke bawah) sedangkan hambatan udara dapat menggerakan mimis ke segala arah tergantung arah dan kecepatan angin. Karena hambatan udara sendiri terutama bersifat sebagai counter-force terhadap gaya gerak mimis (gaya yang melawan, sesuai Hukum Ketiga Newton tentang Aksi-Reaksi), maka mimis akan segera mengalami deselerasi setelah meninggalkan laras.
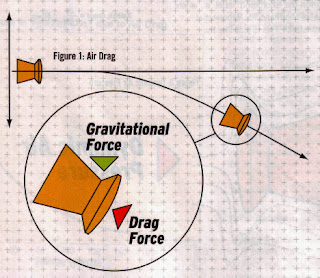 |
| Gambar 2. Gaya yang mempengaruhi mimis selama mimis bergerak dalam lintasannya. Diambil dari http://www.airguns.bg/files/akraba/BC/44550241-The-Ballistic-Coeficient-Explai.pdf |
Dikatakan bahwa deselerasi yang dialami oleh mimis ini berada dalam rasio yang konstan. Artinya untuk setiap jarak yang ditempuh oleh mimis terdapat suatu angka pengurang kecepatan yang tetap. Sebagai contoh: sebuah mimis yang bergerak 600 fps diukur pada ujung larasnya ternyata menunjukkan kecepatan 492 fps pada 10 meter pertama (berarti kecepatannya berkurang 18%), maka bila diukur pada 20 meter mimis ini akan memiliki kecepatan 403 fps (berkurang lagi sebanyak 18%) dan bila diukur lagi pada 30 meter mimis ini akan memiliki kecepatan 337 (berkurang lagi 18%). Pengurangan kecepatan ini terjadi dengan pola yang tetap dan bersifat eksponensial.
Mengetahui bahwa kecepatan mimis berkurang setelah meninggalkan laras, maka kita dapat menentukan kecepatan mimis tersebut pada jarak tertentu. Dan jika kita mengetahui rasio pengurang tersebut, maka kita akan mengetahui di mana mimis akan berhenti bergerak. Jarak yang ditunjukkan saat proyektil ditembakkan sampai proyektil itu diam dinamakan jangkauan balistik. Dalam ilmu balistik jangkauan ini disebut sebagai ballistic range dan biasa dinyatakan dalam satuan yards.
Ballistic Coefficient (BC) pada Mulanya
Perjumpaan pertama saya dengan istilah ini ketika saya mencoba software Chrono Connect Lite. Saat itu saya tidak mengerti dan tidak menyadari seberapa pentingnya faktor dalam istilah ini. Semakin saya mencoba mempelajari istilah ini, semakin saya menyadari keberadaannya dan penggunaannya pada dunia tembak-menembak. Yang saya tahu sebelum saya mencoba menyusun referat ini adalah semakin besar nilai BC suatu proyektil, katakan di atas 1, maka semakin baik proyektil tersebut memelihara energinya dan semakin baik dalam melawan dorongan udara (air drift). Namun pada kenyataannya, BC suatu mimis senapan angin sangat kecil dan tidak akan pernah melebihi nilai 1 (berada di kisaran 0.01-0.03 saja). Jadi apakah semua mimis senapan angin ini sangat buruk dalam desainnya?
Dikatakan pada tahun 1860, seorang Pendeta dari Inggris bernama Francis Bashforth melakukan percobaan pada berbagai proyektil artileri menggunakan pendulum balistik. Menemukan kesulitan dengan banyaknya jenis proyektil saat itu, beliau mengusulkan penggunaan sebuah "proyektil standar" sehingga performa proyektil lain dapat dibandingkan dengan performa proyektil standar tersebut tanpa harus melakukan perhitungan ulang. Hasil performa balistik proyektil yang beliau dapatkan, dinyatakan lebih tinggi atau lebih rendah dibandingkan dengan proyektil standar tersebut. Sebagai konsekuensinya, beliau mengusulkan istilah ballistic coefficient (yang pada intinya adalah hambatan udara/air drag) yang didasarkan pada proyektil standar berbentuk silinder berhidung tumpul, berdiameter 1 inci dan seberat 1 pon (pound atau lb).
Sekitar 20 tahun kemudian yaitu pada tahun 1881, Perusahaan Jerman bernama Krupp melakukan penelitian dengan konsep serupa.dengan proyektil standar yang digunakan sebagai referensi adalah sebuah peluru silinder beralas rata dan berujung tumpul. Proyektil standar ini dinamakan model proyektil standar C. Data yang didapatkan dari penelitian ini dikatakan sangat akurat. Dan oleh seorang insinyur militer Rusia bernama Mayevski data ini dipergunakan untuk menemukan model matematika yang dapat menjelaskan dan memprediksi lintasan (trajectory) peluru tersebut. Kemudian data dari penelitian Krupp dan model matematika dari Mayevski ini, oleh seorang perwira dari angkatan darat Amerika Serikat bernama Kolonel James Ingalls diadaptasi, disederhanakan dan disarikan dalam tabel. Ingalls menggunakan proyetil standar yang hampir mirip dengan milik Krupp dan dinamakan model proyektil G1. Tabel ini dikenal sebagai 'Ingalls Tables' dan dipergunakan oleh personil tentara yang tidak mau terlalu dipusingkan dengan urusan matematika.
Saat ini performa proyektil yang ditembakkan populer dibandingkan dengan proyektil standar model G1 tersebut di atas. Idenya adalah memberikan skala perbandingan performa suatu proyektil dengan performa proyektil G1 tersebut.
Namun saat ini model proyektil lain yang digunakan sebagai standar juga berkembang sesuai dengan berbagai bentuk proyektil yang diproduksi. Dikatakan model G1 hanya akurat dipergunakan untuk menentukan BC suatu proyektil yang memiliki bentuk sejenis dan ditembakan pada kecepatan subsonic (di bawah kecepatan suara, sekitar 350 m/s atau 1100 fps) dengan jarak di bawah 700 yards. Saat ini saja tercatat sudah 11-an model proyektil yang diajukan dan digunakan sebagai proyektil standar untuk menyempurnakan beberapa kelemahan pada model proyektil standar G1. Saat ini produsen peluru banyak yang memilih model proyektil standar G7 yang memiliki ekor seperti bentuk perahu (boat-tail) dan dikatakan lebih dapat menggambarkan lintasan dengan jarak di atas 700 yards. Masalahnya setiap produsen akan mencari BC terbesar yang mereka bisa dapatkan untuk meningkatkan citra performa pelurunya dan tentunya penjualannya.
Untuk menentukan BC suatu proyektil termasuk mimis maka persamaan berikut sangat populer digunakan.
Dikatakan bahwa BC merupakan pembagian dari massa suatu penampang dengan pangkat dua dari kalibernya. Maka besarnya suatu BC sebanding dengan massanya dan berbanding terbalik dengan kwadrat kalibernya. BC sering ditunjukkan tanpa satuan, walaupun sebenarnya memiliki satuannya sendiri. BC dinyatakan dalam satuan lb/in2 atau psi (untuk unit imperial) atau kg/m2 (untuk unit metric).
Sedangkan untuk menentukan Drag Coefficient (CD) diketahui menggunakan persamaan berikut.
 adalah drag force, yang berdasarkan definisi adalah komponen gaya dalam arah kecepatan aliran fluida (dalam hal ini udara).
adalah drag force, yang berdasarkan definisi adalah komponen gaya dalam arah kecepatan aliran fluida (dalam hal ini udara). adalah kepadatan massa fluida, dalam hal ini udara 1 atm pada suhu 20-35 C bernilai ~ 1.15-1.2 kg·m−3.
adalah kepadatan massa fluida, dalam hal ini udara 1 atm pada suhu 20-35 C bernilai ~ 1.15-1.2 kg·m−3. adalah kecepatan obyek relatif terhadap fluida (udara), dalam m/s.
adalah kecepatan obyek relatif terhadap fluida (udara), dalam m/s. adalah area efektif yang berkontak dengan fluida (udara), dalam m3.
adalah area efektif yang berkontak dengan fluida (udara), dalam m3.
Penggunaan jarak balistik dalam rumus untuk menemukan BC yang menggunakan pengertian di atas, ialah:
D1 = Jarak dalam yard, dari muzzle menuju chrono terdekat.
D2 = Jarak dari muzzle menuju chrono yang lebih jauh.
V1 = Kecepatan dalam fps yang diukur dari chrono terdekat.
V2 = Kecepatan yang diukur pada chrono yang lebih jauh.
Penggunaan rumus di atas telah diteliti dan data yang didapatkan menunjukkan hasil yang akurat pada proyektil berbentuk spheris (CD yang digunakan 0.5) dan memiliki kaliber 4.5 mm atau .177". Rumus ini telah digunakan pada banyak kalkulator yang dipergunakan untuk memperkirakan lintasan suatu proyektil. Salah satu yang populer di kalangan penembak senapan angin adalah Software keluaran Hawke Sports yang dinamakan ChairgunPro.
Jadi Apakah Sebenarnya Ballistic Coefficient Itu?
Sebenarnya BC adalah rasio pengurangan kecepatan akibat tahanan udara pada proyektil tertentu yang dibandingkan dengan proyektil standar G. Dengan mengetahui kecepatan proyektil/mimis pada dua jarak yang berbeda, kita bisa menentukan BC proyektil atau mimis yang kita hendak ukur. Hal ini melibatkan dua buah chronograph yang ditempatkan pada dua jarak yang sudah ditentukan sebelumnya. Satu pada jarak yang dekat dan satu lagi pada jarak yang lebih jauh.
Dikatakan metoda terbaik untuk menentukan BC ini adalah dengan mengukur sendiri kecepatan dari proyektil/mimis yang ditembakan oleh laras senapan sendiri pada dua titik yang dekat dan jauh menggunakan dua buah chronograph. Hal ini untuk menyingkirkan perbedaan CD akibat deformitas mimis yang tercipta selama mimis bergerak sepanjang alur laras.
Simpulan dan Penutup
Saya menyadari dengan keterbatasan intelejensi dan kompetensi saya, akan ada kesalahan dalam mengutip dan menarik simpulan mengenai topik yang sulit ini. Catatan yang saya buat dan publikasikan ini walaupun cukup untuk memuaskan keingintahuan saya, namun berpotensi menimbulkan lebih banyak pertanyaan dan koreksi dari pembaca yang lebih kompeten di bidang ini. Saya menyarankan pembaca mempelajari langsung dari sumbernya yang saya cantumkan pada akhir artikel ini untuk memberi wacana dan pengertian lebih lengkap. Dan tolong koreksi kesalahan saya.
Pada artikel selanjutnya saya akan mengulas penggunaan ballistic coefficient ini dalam praktek menembak yang lebih berguna dalam keseharian kita.
Ballistic Coefficient (BC) pada Mulanya
Perjumpaan pertama saya dengan istilah ini ketika saya mencoba software Chrono Connect Lite. Saat itu saya tidak mengerti dan tidak menyadari seberapa pentingnya faktor dalam istilah ini. Semakin saya mencoba mempelajari istilah ini, semakin saya menyadari keberadaannya dan penggunaannya pada dunia tembak-menembak. Yang saya tahu sebelum saya mencoba menyusun referat ini adalah semakin besar nilai BC suatu proyektil, katakan di atas 1, maka semakin baik proyektil tersebut memelihara energinya dan semakin baik dalam melawan dorongan udara (air drift). Namun pada kenyataannya, BC suatu mimis senapan angin sangat kecil dan tidak akan pernah melebihi nilai 1 (berada di kisaran 0.01-0.03 saja). Jadi apakah semua mimis senapan angin ini sangat buruk dalam desainnya?
Dikatakan pada tahun 1860, seorang Pendeta dari Inggris bernama Francis Bashforth melakukan percobaan pada berbagai proyektil artileri menggunakan pendulum balistik. Menemukan kesulitan dengan banyaknya jenis proyektil saat itu, beliau mengusulkan penggunaan sebuah "proyektil standar" sehingga performa proyektil lain dapat dibandingkan dengan performa proyektil standar tersebut tanpa harus melakukan perhitungan ulang. Hasil performa balistik proyektil yang beliau dapatkan, dinyatakan lebih tinggi atau lebih rendah dibandingkan dengan proyektil standar tersebut. Sebagai konsekuensinya, beliau mengusulkan istilah ballistic coefficient (yang pada intinya adalah hambatan udara/air drag) yang didasarkan pada proyektil standar berbentuk silinder berhidung tumpul, berdiameter 1 inci dan seberat 1 pon (pound atau lb).
Sekitar 20 tahun kemudian yaitu pada tahun 1881, Perusahaan Jerman bernama Krupp melakukan penelitian dengan konsep serupa.dengan proyektil standar yang digunakan sebagai referensi adalah sebuah peluru silinder beralas rata dan berujung tumpul. Proyektil standar ini dinamakan model proyektil standar C. Data yang didapatkan dari penelitian ini dikatakan sangat akurat. Dan oleh seorang insinyur militer Rusia bernama Mayevski data ini dipergunakan untuk menemukan model matematika yang dapat menjelaskan dan memprediksi lintasan (trajectory) peluru tersebut. Kemudian data dari penelitian Krupp dan model matematika dari Mayevski ini, oleh seorang perwira dari angkatan darat Amerika Serikat bernama Kolonel James Ingalls diadaptasi, disederhanakan dan disarikan dalam tabel. Ingalls menggunakan proyetil standar yang hampir mirip dengan milik Krupp dan dinamakan model proyektil G1. Tabel ini dikenal sebagai 'Ingalls Tables' dan dipergunakan oleh personil tentara yang tidak mau terlalu dipusingkan dengan urusan matematika.
| Gambar 3. Model Proyektil Standar "C" oleh Krupp. Angka yang ditunjukkan adalah perkalian dengan ukuran diameter peluru/kaliber. Pada kaliber 1" maka didapatkan panjang 3", panjang badan silinder 1.7", dan radius (jari-jari) lingkaran hidung sebesar 1.49". Diambil dari http://www.frfrogspad.com/drgshape.htm. |
| Gambar 4. Model Proyektil Standar "G1" oleh Ingalls. Ukuran yang tercantum merupakan perkalian dengan kaliber peluru. Diambil dari http://www.frfrogspad.com/drgshape.htm. |
Saat ini performa proyektil yang ditembakkan populer dibandingkan dengan proyektil standar model G1 tersebut di atas. Idenya adalah memberikan skala perbandingan performa suatu proyektil dengan performa proyektil G1 tersebut.
Namun saat ini model proyektil lain yang digunakan sebagai standar juga berkembang sesuai dengan berbagai bentuk proyektil yang diproduksi. Dikatakan model G1 hanya akurat dipergunakan untuk menentukan BC suatu proyektil yang memiliki bentuk sejenis dan ditembakan pada kecepatan subsonic (di bawah kecepatan suara, sekitar 350 m/s atau 1100 fps) dengan jarak di bawah 700 yards. Saat ini saja tercatat sudah 11-an model proyektil yang diajukan dan digunakan sebagai proyektil standar untuk menyempurnakan beberapa kelemahan pada model proyektil standar G1. Saat ini produsen peluru banyak yang memilih model proyektil standar G7 yang memiliki ekor seperti bentuk perahu (boat-tail) dan dikatakan lebih dapat menggambarkan lintasan dengan jarak di atas 700 yards. Masalahnya setiap produsen akan mencari BC terbesar yang mereka bisa dapatkan untuk meningkatkan citra performa pelurunya dan tentunya penjualannya.
Untuk menentukan BC suatu proyektil termasuk mimis maka persamaan berikut sangat populer digunakan.
- BCBullets = ballistic coefficient.
- SD = sectional density, SD = massa dari peluru/proyekti dalam pound atau kilogram dibagi dengan kaliber dikwadratkan dalam inchi atau meter.
- i = form factor, i =
; (CG ~ 0.5191).
- CB = Drag coefficient dari peluru/proyektil yang diukur.
- CG = Drag coefficient dari proyektil standar model G1.
- M = Massa peluru atau proyektil, lb atau kg
- d = diameter peluru, in atau m
Dikatakan bahwa BC merupakan pembagian dari massa suatu penampang dengan pangkat dua dari kalibernya. Maka besarnya suatu BC sebanding dengan massanya dan berbanding terbalik dengan kwadrat kalibernya. BC sering ditunjukkan tanpa satuan, walaupun sebenarnya memiliki satuannya sendiri. BC dinyatakan dalam satuan lb/in2 atau psi (untuk unit imperial) atau kg/m2 (untuk unit metric).
Sedangkan untuk menentukan Drag Coefficient (CD) diketahui menggunakan persamaan berikut.
Dari persamaan di atas diketahui bahwa CD berbalik terbalik dengan pangkat dua kecepatan dan luas area efektif.
Beberapa Kelemahan Perhitungan Ballistic Coefficient Berbasis CD
Kelemahan pendekatan menggunakan rumus BC berbasis CD di atas yaitu model proyektil standar yang digunakan sebagai pembanding memiliki bentuk conical (kerucut). Sedangkan seperti kita ketahui bahwa suatu mimis yang berbentuk diabolo (dua bola) memiliki area efektif berbentuk spherical (bola atau setengah bola) sehingga CD pada bentuk ini pasti memiliki nilai yang berbeda (sekitar 0.42-0.47, nilai CD dari bentuk setengah bola dan bola). Akibatnya dalam aplikasinya di dunia nyata menggunakan berbagai bentuk proyektil, hasil perhitungan lintasan yang didapatkan tidak sesuai dengan kenyataannya.
Kelemahan lain yang didapatkan adalah dari berbagai data penelitian dikatahui bahwa CD berubah seiring dengan berubahnya kecepatan. Berikut ini salah satu gambar yang menarik untuk menggambarkan perubahan CD pada kecepatan yang berbeda dari sebuah mimis berdiameter 4.5 mm.
Atau pada penggunaan riil di dunia senapan angin, ada pula data yang menarik untuk menunjukkan perubahan BC akibat perbedaan kecepatan mimis. Hasil selengkapnya dapat disimak di sini.
Lalu CD suatu mimis juga akan berbeda nilainya setelah mimis mengalami deformitas dalam laras. Bayangkan suatu bentuk spheris mimis berubah menjadi bergerigi karena cetakan rifling dalam laras yang tentunya akan merubah CD area efektif mimis tersebut. Belum lagi seperti diulas sebelumnya, mimis saat meninggalkan laras akan mengalami gerakan sepanjang lintasannya. Gerakan berputar seperti yawing dan precession dalam berbagai sudut tentunya akan mempengaruhi CD yang diukur. Saya menyerah untuk memikirkannya sampai sejauh ini.
Jarak Balistik sebagai penentu Ballistic Coefficient
Telah saya singgung sebelumnya bahwa kecepatan mimis yang ditembakkan akan mengalami deselerasi dengan rasio yang tetap. Kenyataan ini menggambarkan bahwa hambatan udara mengurangi kecepatan proyektil dengan rasio yang tetap.
Grafik di atas menunjukkan rasio pengurangan kecepatan terhadap jarak yang ditempuh oleh suatu proyektil. Bentuk grafik yang sama ditemukan pula pada berbagai fenomena alam. Sebagai contohnya yaitu pola hubungan aktifitas peluruhan radioaktif karbon yang mendasari perhitungan usia karbon (carbon dating) suatu artifak, hubungan antara kerapatan lingkaran hujan pada suatu batang pohon, bahkan hubungan penurunan nilai mata uang pada tingkat inflasi yang tetap. Fenomena ini dapat diukur dan membentuk pola grafik di atas. Bentuk pola di atas merupakan pola logaritma yang disebut logaritma alami (natural logarithm). Pola ini diungkapkan oleh seorang ahli matematika, fisika dan astronomi bernama John Napier sehingga disebut pula logaritma Napier. Nilai konstanta eksponen yang didapatkan dari perhitungan logaritma ini sebesar 2.7183 dan diberi lambang "e".
Menyadari keberadaan fenomena di atas pada hubungan kecepatan proyektil terhadap jarak, dari data yang yang dikumpulkan oleh tabel Ingalls ditemui bahwa pada jarak 8000 yards, pada proyektil yang memiliki BC sebesar 1.000 (satu) akan mengalami perlambatan sebesar 63% atau hanya menyisakan 37% dari kecepatan awalnya. Dengan membandingkan (membagi) jarak balistik dengan 8000 ini berarti menempatkan jarak balistik proyektil yang diukur dalam jangkauan logaritma alami menggunakan pembanding proyektil standar model G.Beberapa Kelemahan Perhitungan Ballistic Coefficient Berbasis CD
Kelemahan pendekatan menggunakan rumus BC berbasis CD di atas yaitu model proyektil standar yang digunakan sebagai pembanding memiliki bentuk conical (kerucut). Sedangkan seperti kita ketahui bahwa suatu mimis yang berbentuk diabolo (dua bola) memiliki area efektif berbentuk spherical (bola atau setengah bola) sehingga CD pada bentuk ini pasti memiliki nilai yang berbeda (sekitar 0.42-0.47, nilai CD dari bentuk setengah bola dan bola). Akibatnya dalam aplikasinya di dunia nyata menggunakan berbagai bentuk proyektil, hasil perhitungan lintasan yang didapatkan tidak sesuai dengan kenyataannya.
Kelemahan lain yang didapatkan adalah dari berbagai data penelitian dikatahui bahwa CD berubah seiring dengan berubahnya kecepatan. Berikut ini salah satu gambar yang menarik untuk menggambarkan perubahan CD pada kecepatan yang berbeda dari sebuah mimis berdiameter 4.5 mm.
 |
| Gambar 5. Variasi Drag Coefficient pada berbagai kecepatan. Diambil dari http://www.network54.com/Forum/79537/thread/1254669078/Ballistic+Coefficients+based+on+G1+model-%60 |
Atau pada penggunaan riil di dunia senapan angin, ada pula data yang menarik untuk menunjukkan perubahan BC akibat perbedaan kecepatan mimis. Hasil selengkapnya dapat disimak di sini.
Lalu CD suatu mimis juga akan berbeda nilainya setelah mimis mengalami deformitas dalam laras. Bayangkan suatu bentuk spheris mimis berubah menjadi bergerigi karena cetakan rifling dalam laras yang tentunya akan merubah CD area efektif mimis tersebut. Belum lagi seperti diulas sebelumnya, mimis saat meninggalkan laras akan mengalami gerakan sepanjang lintasannya. Gerakan berputar seperti yawing dan precession dalam berbagai sudut tentunya akan mempengaruhi CD yang diukur. Saya menyerah untuk memikirkannya sampai sejauh ini.
Jarak Balistik sebagai penentu Ballistic Coefficient
Telah saya singgung sebelumnya bahwa kecepatan mimis yang ditembakkan akan mengalami deselerasi dengan rasio yang tetap. Kenyataan ini menggambarkan bahwa hambatan udara mengurangi kecepatan proyektil dengan rasio yang tetap.
 |
| Gambar 6. Hubungan Penurunan Kecepatan Seiring Jarak yang Ditempuh Akibat Hambatan Udara (Air Drag). Diambil dari http://www.airguns.bg/files/akraba/BC/44550241-The-Ballistic-Coeficient-Explai.pdf |
Grafik di atas menunjukkan rasio pengurangan kecepatan terhadap jarak yang ditempuh oleh suatu proyektil. Bentuk grafik yang sama ditemukan pula pada berbagai fenomena alam. Sebagai contohnya yaitu pola hubungan aktifitas peluruhan radioaktif karbon yang mendasari perhitungan usia karbon (carbon dating) suatu artifak, hubungan antara kerapatan lingkaran hujan pada suatu batang pohon, bahkan hubungan penurunan nilai mata uang pada tingkat inflasi yang tetap. Fenomena ini dapat diukur dan membentuk pola grafik di atas. Bentuk pola di atas merupakan pola logaritma yang disebut logaritma alami (natural logarithm). Pola ini diungkapkan oleh seorang ahli matematika, fisika dan astronomi bernama John Napier sehingga disebut pula logaritma Napier. Nilai konstanta eksponen yang didapatkan dari perhitungan logaritma ini sebesar 2.7183 dan diberi lambang "e".
Penggunaan jarak balistik dalam rumus untuk menemukan BC yang menggunakan pengertian di atas, ialah:
BC = (D2 - D1) / [8000 * LOGe(V1/V2)]
D2 = Jarak dari muzzle menuju chrono yang lebih jauh.
V1 = Kecepatan dalam fps yang diukur dari chrono terdekat.
V2 = Kecepatan yang diukur pada chrono yang lebih jauh.
Penggunaan rumus di atas telah diteliti dan data yang didapatkan menunjukkan hasil yang akurat pada proyektil berbentuk spheris (CD yang digunakan 0.5) dan memiliki kaliber 4.5 mm atau .177". Rumus ini telah digunakan pada banyak kalkulator yang dipergunakan untuk memperkirakan lintasan suatu proyektil. Salah satu yang populer di kalangan penembak senapan angin adalah Software keluaran Hawke Sports yang dinamakan ChairgunPro.
Jadi Apakah Sebenarnya Ballistic Coefficient Itu?
Sebenarnya BC adalah rasio pengurangan kecepatan akibat tahanan udara pada proyektil tertentu yang dibandingkan dengan proyektil standar G. Dengan mengetahui kecepatan proyektil/mimis pada dua jarak yang berbeda, kita bisa menentukan BC proyektil atau mimis yang kita hendak ukur. Hal ini melibatkan dua buah chronograph yang ditempatkan pada dua jarak yang sudah ditentukan sebelumnya. Satu pada jarak yang dekat dan satu lagi pada jarak yang lebih jauh.
Dikatakan metoda terbaik untuk menentukan BC ini adalah dengan mengukur sendiri kecepatan dari proyektil/mimis yang ditembakan oleh laras senapan sendiri pada dua titik yang dekat dan jauh menggunakan dua buah chronograph. Hal ini untuk menyingkirkan perbedaan CD akibat deformitas mimis yang tercipta selama mimis bergerak sepanjang alur laras.
Simpulan dan Penutup
- Gaya yang bekerja pada suatu mimis setelah meninggalkan laras adalah gaya gravitasi dan hambatan udara (air drag).
- Kecepatan proyektil (mimis) berkurang dengan rasio yang tetap setelah proyektil tersebut meninggalkan laras.
- Hubungan kecepatan dengan jarak yang ditempuh bersifat eksponensial.
- Ballistic Coefficient adalah rasio perbandingan pengurangan kecepatan akibat hambatan udara yang dibandingkan dengan proyektil standar G.
- Ballistic Coefficient menggambarkan performa suatu proyektil (mimis) terhadap pengaruh hambatan udara (air drag)..
- Nilai Ballistic Coefficient terbaik didapatkan dengan mengukur sendiri kecepatan yang didapatkan menggunakan proyektil (mimis) yang ditembakkan dari laras senapan sendiri dengan menggunakan dua chronograph.
Saya menyadari dengan keterbatasan intelejensi dan kompetensi saya, akan ada kesalahan dalam mengutip dan menarik simpulan mengenai topik yang sulit ini. Catatan yang saya buat dan publikasikan ini walaupun cukup untuk memuaskan keingintahuan saya, namun berpotensi menimbulkan lebih banyak pertanyaan dan koreksi dari pembaca yang lebih kompeten di bidang ini. Saya menyarankan pembaca mempelajari langsung dari sumbernya yang saya cantumkan pada akhir artikel ini untuk memberi wacana dan pengertian lebih lengkap. Dan tolong koreksi kesalahan saya.
Pada artikel selanjutnya saya akan mengulas penggunaan ballistic coefficient ini dalam praktek menembak yang lebih berguna dalam keseharian kita.
No comments:
Post a Comment